Okay, picture this: a tree with branches, but instead of leaves, it has numbers and it's upside down. And the first number is called the root node. Use this image so I don't annoy you

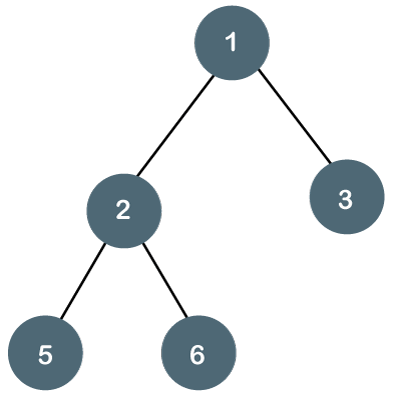
Two numbers are branching from the root node

Those 2 branches form parent nodes other to other children

Let us use a more complex one

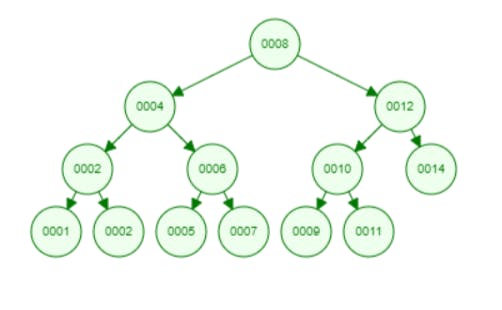
The numbers are not randomly arranged. On every branch, the value on the left is smaller than the one on the parent node and the value on the right is larger than the parent node.

And yes the first image of this article is not a valid binary tree.

You can create your own binary tree here to see how it works

Anyway, the binary tree is made that way to help for easy searching

As you search, the number of values you have to search through is divided in half. That is the secret to its speed!

Let us go straight to how we can implement this in python

I recommend you have decent knowledge in Object Oriented Programming (OOP) for this.

class Node:
    def __init__(self, key):
        self.left = None
        self.right = None
        self.val = key

class BST:
    def __init__(self):
        self.root = None

    def insert(self, root, key):
        if root is None:
            return Node(key)
        else:
            if key < root.val:
                root.left = self.insert(root.left, key)
            else:
                root.right = self.insert(root.right, key)
        return root

    def search(self, key):
        if self.root is None or root.val == key:
            return root

        if self.root.val < key:
            return self.search(self.root.right, key)

        return self.search(self.root.left, key)

We have 2 classes
BST which stands for Binary Search Tree and Node which stands for .... node👍

When trying to add something to the tree, we make sure it follows the rules so that retrieving it is not a hassle. This is what the insert function, is trying to achieve

The search function is supposed to get any value that you're looking for in the binary tree (Recursively). This works similarly to how it is sorted when added.

# Create a BST instance
bst = BST()

# Insert elements
keys = [15, 10, 20, 8, 12, 17, 25]
for key in keys:
    bst.root = bst.insert(bst.root, key)

search_value = 12
result_node = bst.search(bst.root, search_value)

if result_node:
    print(f"Value {search_value} found in the tree!")
else:
    print(f"Value {search_value} not found in the tree.")

This is just an example of how you can run the binary tree you just implemented and search for a value in it

Conclusion

In the realm of Binary Search Trees (BSTs), we've unveiled a powerful tool that balances simplicity and efficiency. With the rule of smaller left and larger right, BSTs enable lightning-fast data searches and structured organization.

In the tech world, BSTs shine as unsung heroes. They underpin search engines, database systems, and more at big tech companies. Their balance and speed drive the algorithms that power our digital interactions, making BSTs an essential foundation of modern technology.